搜尋

暴力的把每種可能性都列出來，然後把所想要的東西留下，就是搜尋的原點。

不彷將搜尋所能觸及到的可能性稱為狀態
每當狀態改變後，前個狀態到下個狀態的過程稱狀態轉移。
若把狀態看作點，而狀態轉移看作邊，包含這些點與邊的圖稱作狀態空間
建議複習圖論術語

從格鬥遊戲來看，每一次出重拳輕拳輕踢扣血跳躍等等的，或是敵人與自己大招的能量條，都是一種狀態，而角色從閒置到出拳則是一種狀態轉移，且所有的招式組合構成了狀態空間。

根據狀態空間規模，須用一些手段使得能更快速的找到所想要的東西。

本章使用的圖論符號慣例：

• E (Edge) 表邊集合，通常起點用 u、終點用 v 作為節點符號
• V (Vertex) 表節點集合，表達單一節點常用 u, v

DFS

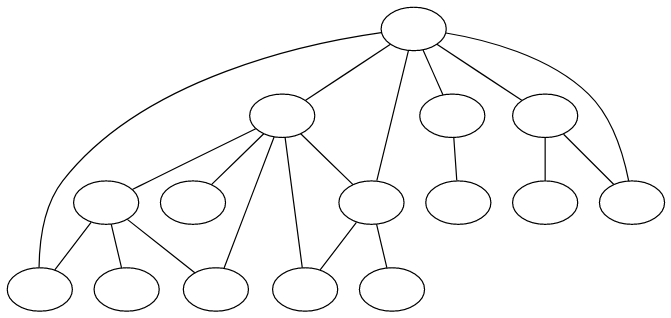
深度優先搜尋 (Depth-first Search) 簡稱 DFS，是優先往深度大的節點走訪。
這裡的走訪為走遍所有點，若中途碰到曾走過的點不往下繼續走。

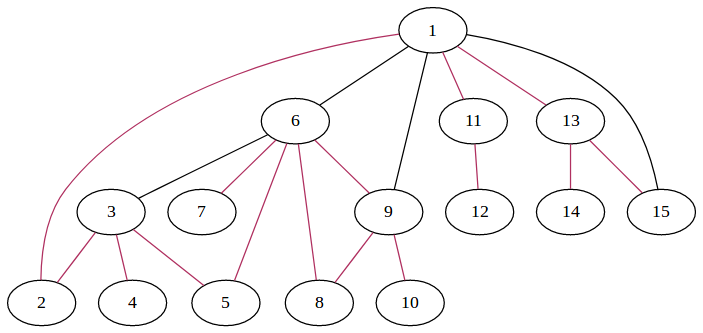
按照上圖，走訪順序為最小的數字 1 依照正整數列開始走訪到 15。

DFS 走過的路經為一棵樹，稱此樹為 DFS 樹。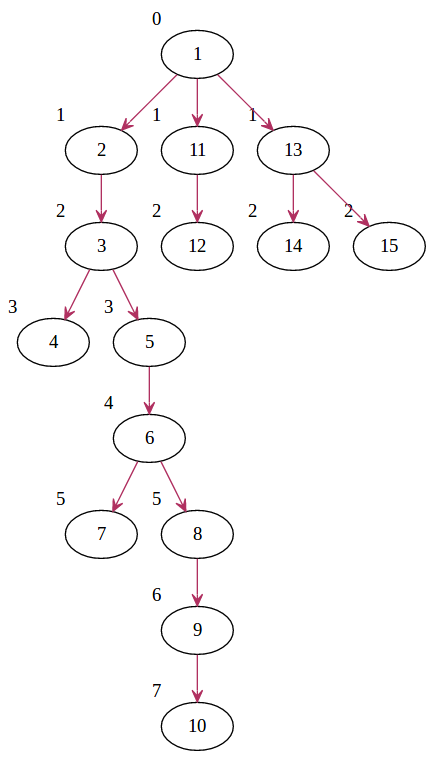

(其中節點左上角數字代表深度)

void dfs(int u, int dep) { // dep := depth
  for (auto v: E[u]) {
    if (vis[v]) continue;
    vis[v] = true;
    dfs(v, dep+1);
  }
}

其中 vis[i] (這個變數將當作以後的慣例) 為 true 代表此節點已經拜訪過，下次不考慮此節點為更深的子孫節點。

DFS 除了能夠以上述遞迴方式呈現，也可以採用 stack 來實做，
而實際上這兩種作法在本質上是相同的，請讀者稍微思考看看。

stack<int> S;

while(!S.empty()) {
  int u = S.top(); S.pop();
  
  for (auto v: E[u]) {
    if (vis[v]) continue;
    vis[v] = true;
    S.push(v);
  }
}

狀態搜尋

搜尋某個狀態，可以利用函式與參數表示，例如會把 f(1, 2, 3) 和 f(3, 4, 5) 這樣的函式呼叫，當作不同的狀態去接觸(求解)它。

範題 UVa OJ 572 Oil Deposits：

題目要求一個區域中有幾個連通圖
所謂的連通，就是圖中任意兩點間至少有一條路徑

當接觸到 dfs(r, c) 這個狀態時，代表這裡有塊包含座標 的 oil deposit (前提是 plot[r][c] 為 '@')
而 DFS 走訪時，只需確保不再重複走到走過的點，所以走過就設 '*'

void dfs(int r, int c)
{
  if(plot[r][c] == '*') return;
  plot[r][c] = '*';

  for (int dr = -1; dr <= 1; dr++)
    for (int dc = -1; dc <= 1; dc++) //雙重迴圈讓八個方位都走
      if (r+dr >= 0 && r+dr < m && c+dc >= 0 && c+dc < n)
        dfs(r+dr, c+dc);
}

只要是連通圖，DFS 都能把此圖走訪完
這裡簡單算走進幾次連通圖就好

int count = 0;
for (int i = 0; i < m; i++)
  for (int j = 0; j < n; j++)
    if (plot[i][j] == '@') { dfs(i, j); count++; }

下回應該會談 BFS，咱們改天見！